Word Level Semantics
Count-based methods
- Define a basis vocabulary \(C\) of context words
- Define a word window size \(w\)
- Count the basis vocabulary words occurring \(w\) words to the left or right of each instance of a target word in the corpus.
- Form a vector representation of the target word based on these counts.
Example:
- ... and the cute kitten purred and then ...
- ... the cute furry cat purred and miaowed ...
- ... that the small kitten miaowed and she ...
- ... the loud furry dog ran and bit ...
Example basis vocabulary: {bit, cute, furry, loud, miaowed, purred, ran, small}.
- kitten context words: {cute, purred, small, miaowed}.
- cat context words: {cute, furry, miaowed}.
- dog context words: {loud, furry, ran, bit}.
Therefore
- \(kitten = [0, 1, 0, 0, 1, 1, 0, 1]^T\)
- \(cat = [0, 1, 1, 0, 1, 0, 0, 0]^T\)
- \(dog = [1, 0, 1, 1, 0, 0, 1, 0]^T\)
Neural Embedding Models
Learning count based vetors produces an embedding matrix \(E\) in \(R^{|vocab|*|context|}\).

Rows are word vectors = one hot vector
- \(cat = onehot^T_{cat}E\)
General idea behind embedding learning:
- Collect instances \(t_i \in inst(t)\) of a word \(t\) of vocab \(V\)
- For each instance, collect its context words \(c(t_i)\) (e.g. k-word window)
- Define some score function \(socre(t_i, c(t_i); \theta, E)\) with upper bound on output
- Define a loss
- Estimate
- Use the estimated \(E\) as your embedding matrix
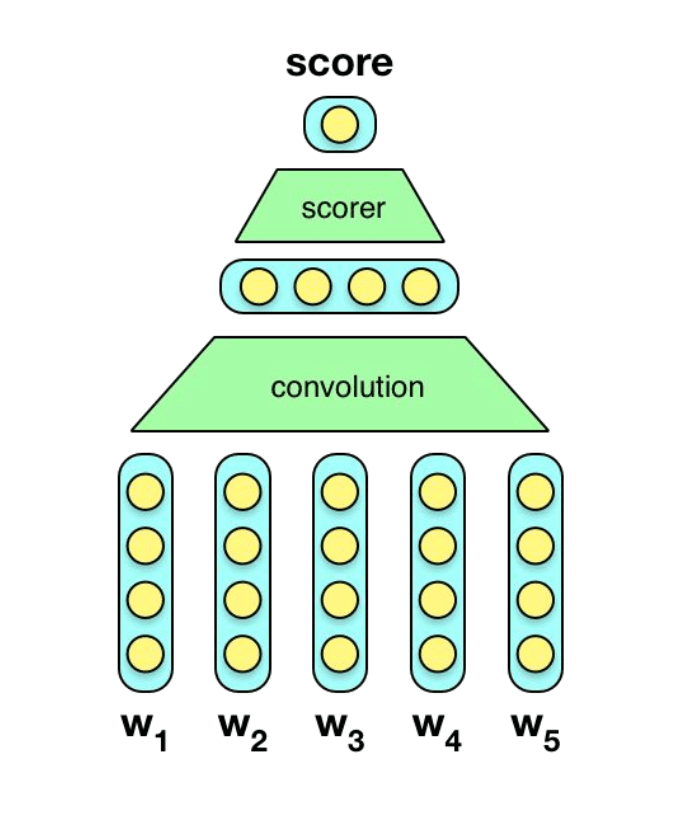
C&W
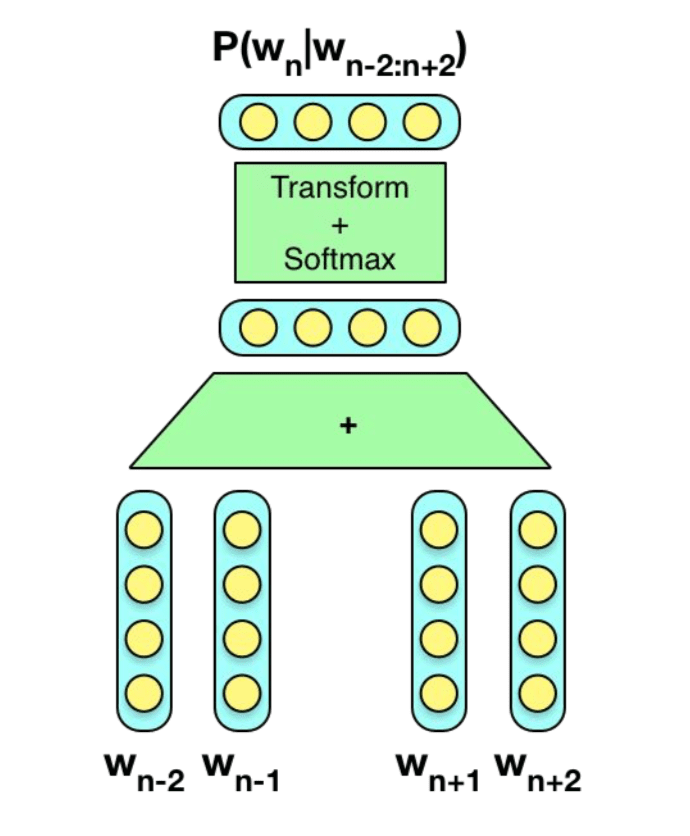
CBoW
word2vec详解:http://blog.csdn.net/itplus/article/details/37969979
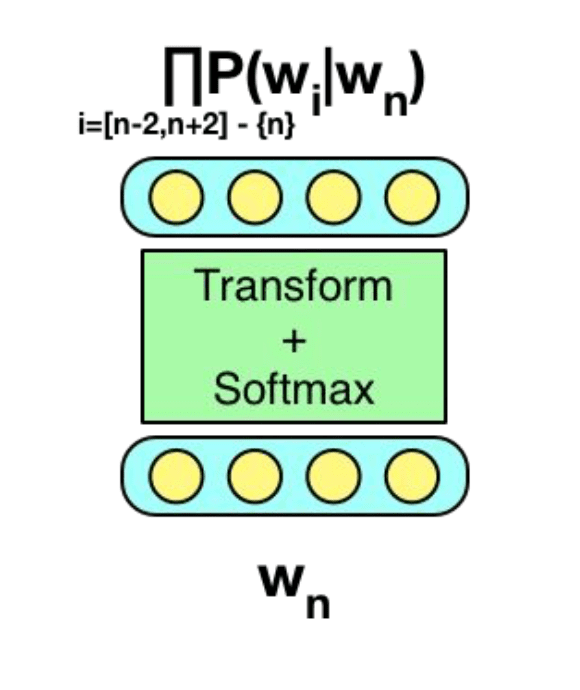
Skip-gram
Task-based Embedding Learning
Neural network parameters are updated using gradients on loss \(L(x, y, \theta)\) \[ \theta_{t+1} = update(\theta_t, \triangledown_\theta L(x, y, \theta_t)) \] If \(E \in \theta\) then this update can modify \(E\) : \[ E_{t+1} = update(E_t, \triangledown_E L(x, y, \theta_t)) \] General intuition: learn to classify/predict/generate based on features, but also the features themselves.
- Bow Classifiers
- Bilingual Features