In statistics, an expectation–maximization (EM) algorithm is an iterative method for finding maximum likelihood or maximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables.
直观理解高斯混合模型(GMM)
最大似然估计
最大似然估计(Maximum Likelihood Estimation, MLE)是为了找出找出与样本的分布最接近的概率分布模型。
ps : 熟悉最大似然估计的同学可以跳过这部分 :)
举个简单的例子:10次抛硬币的结果是: 正正反正正正反反正正。假设 \(p\) 是每次抛硬币结果为正的概率。则得到这样的实验结果的概率是: \[P = pp(1-p)ppp(1-p)(1-p)pp = p^7(1-p)^3\] 最大化 \(P\) 解得最优解是 \(p = 0.7\),与直观感觉 \(p = \frac{正面次数}{抛的次数} = \frac{7}{10} = 0.7\) 一致。
二项分布的最大似然估计
对上面的例子简单推广一下:投硬币试验中,进行 \(N\) 次独立试验,\(n\) 次朝上, \(N-n\)次朝下。假定朝上的概率为 \(p\), 使用对数似然函数作为目标函数: \[f(n\ |\ p) = \log(p^n(1-p)^{N-n})\]
对 \(p\) 求偏导并令其等于零,求对数似然函数最大时 \(p\) 的值:
\[\begin{array}{lcr} \frac{\partial f(n\ |\ p)}{\partial p} = \frac{n}{p} - \frac{N-n}{1-p} = 0 \\ \Rightarrow p = \frac{n}{N} \end{array}\]
高斯分布的最大似然估计
进一步考虑,若给定一组样本 \(x_1,x_2...x_n\), 已知它们来自于高斯分布 \(N(μ,σ)\), 试估计参数 \(μ,σ\)。
高斯分布的概率密度函数 : \[f(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(x-\mu)^2}{2\sigma^2})\]
将 \(X_i\) 的样本值 \(x_i\) 带入, 得到似然函数 :
\[L(x) = \prod_{i=1}^n\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(x_i-\mu)^2}{2\sigma^2})\]
取对数并化简得:
\[\begin{array}{lcr} l(x) = \log \prod_{i=1}^n\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(x_i-\mu)^2}{2\sigma^2}) \\ \ \ \ \ \ = \sum_{i=1}^n\log\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(x_i-\mu)^2}{2\sigma^2}) \\ \ \ \ \ \ = \sum_{i=1}^n \log\frac{1}{\sqrt{2\pi}\sigma} + \sum_{i=1}^n-\frac{(x_i-\mu)^2}{2\sigma^2} \\ \ \ \ \ \ = -\frac{n}{2}\log(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2 \end{array}\]
最大化上述对数似然函数,即对 \(\mu\) 和 \(\sigma\) 求偏导并令其等于零,解得:
\[\begin{cases} \mu = \frac{1}{n}\sum_{i=1}^nx_i \\ \sigma^2 = \frac{1}{n}\sum_{i=1}^n(x_i - \mu)^2 \end{cases}\]
这两个值就是样本均值和样本方差,和矩估计的结果是一致的,并且意义非常直观:样本的均值即高斯分布的均值, 样本的伪方差即高斯分布的方差。
问题 : 随机变量无法直接(完全)观察到
随机挑选10000位志愿者,测量他们的身高: 若样本中存在男性和女性,身高分别服从 \(N(μ_1,σ_1)\) 和 \(N(μ_2,σ_2)\) 的分布,试估计 \(μ_1,σ_1,μ_2,σ_2\) 。
更加一般化的描述如下:随机变量 \(X\) 是有 \(K\) 个高斯分布混合而成,取各个高斯分布的概率(权值)为 \(π_1,π_2... π_K\),第 \(i\) 个高斯分布的均值为 \(μ_i\),方差为 \(Σ_i\)。若观测到随机变量 \(X\) 的一系列样本 \(x_1,x_2,...,x_n\),试估计参数 \(π\),\(μ\),\(Σ\)。
建立目标对数似然函数:
\[l_{\pi,\mu,\Sigma}(x) = \sum_{i=1}^N\log(\sum_{k=1}^K\pi_kN(x_i\ |\ \mu_k, \Sigma_k))\]
由于在对数函数里面又有加和,我们没法直接用求导解方程的办法直接求得最大值。为了解决这个问题,我们分成两步。
第一步 : 估算数据来自哪个组份
估计数据由每个组份生成的概率 : 对于每个样本 \(x_i\),它由第 \(k\) 个组份生成的概率为
\[\gamma(i, k) = \frac{\pi_kN(x_i\ |\ \mu_k, \Sigma_k)}{\sum_{j=1}^K\pi_jN(x_i\ |\ \mu_j, \Sigma_j)}\]
上式中的 \(μ\) 和 \(Σ\) 也是待估计的值,因此采样迭代法: 在计算 \(γ(i,k)\) 时假定 \(μ\) 和 \(Σ\) 已知; \(γ(i,k)\) 亦可看成组份 \(k\) 在生成数据 \(x_i\) 时所做的贡献。
第二步 : 估计每个组份的参数
对于所有的样本点,对于组份 \(k\) 而言,可看做生成了 \(\{\gamma(i, k)x_i\ |\ i = 1,2,...N\}\) 这些点。组份 \(k\) 是一个标准的高斯分布,利用上面的结论可以得出:
\[\begin{cases} N_k = \sum_{i=1}^N\gamma(i, k) \\ \mu_k = \frac{1}{N_k}\sum_{i=1}^N\gamma(i,k)x_i \\ \Sigma_k = \frac{1}{N_k}\sum_{i=1}^N\gamma(i,k)(x_i - \mu_k)(x_i-\mu_k)^T \\ \pi_k = \frac{N_k}{N} = \frac{1}{N}\sum_{i=1}^N\gamma(i, k) \end{cases}\]
然后就可以迭代了,我们先拍脑门给一个 \(\gamma(i, k)\) ,然后在已知 \(\gamma\) 的情况下计算第二步四个量,然后再代入第一步更新 \(\gamma\),然后再计算第二步 ... 如此往复,直到收敛。
EM算法
其实上述的高斯混合模型就是EM算法的一个应用,接下来我们用公式正式推导一下EM算法。
EM算法的提出
假定有训练集 \(\{x^{(1)}, x^{(2)}, ... , x^{(m)}\}\),包含 \(m\) 个独立样本,希望从中找到该组数据的模型 \(p(x,z)\) 的参数,其中 \(z\) 是一个隐变量。
通过最大似然估计建立目标函数
\[l(\theta) = \sum_{i=1}^m\log p(x\ ;\theta) = \sum_{i=1}^m\log \sum_z p(x,z;\theta)\]
由于 \(z\) 是隐随机变量,不方便直接找到参数估计。所以我们采用以下策略:计算 \(l(θ)\) 下界,求该下界的最大值;重复该过程,直到收敛到局部最大值。
如下图所示,\(P(x\ |\ \theta)\) 是我们的目标函数,我们想在绿线那个点的下方找到一个函数 \(r(x\ |\ \theta)\),使 \(r(x\ |\ \theta)\) 严格小于 \(P(x\ |\ \theta)\),并且我们希望在绿线那个点上 \(r(x\ |\ \theta) = P(x\ |\ \theta)\)。找到了 \(r(x\ |\ \theta)\) 之后我们可以求 \(r(x\ |\ \theta)\) 的最大值,也就是红线处,然后重复以上步骤,直到收敛到局部最大值。
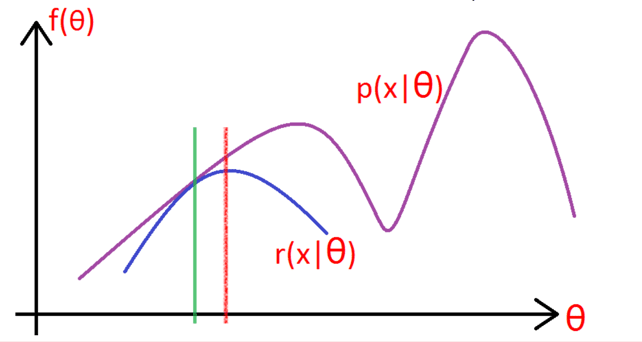
Jensen不等式
在推导如何找下界 \(r(x\ |\ \theta)\) 之前,先来看一下Jensen不等式,等下要用到。
若 \(f\) 是凸函数,则: \[f(\theta x + (1 - \theta) y) \leqslant \theta f(x) + (1-\theta)f(y) \]
把上推广一下,若 \(\theta_1, ..., \theta_k \geqslant 0, \ \theta_1 + ... + \theta_k = 1\),则: \[f(\theta_1x_1 + ... + \theta_k\theta_k) \leqslant \theta_1f(x_1) + ... + \theta_kf(x_k)\]
\(\theta_i\) 也可以看作是 \(x_i\) 发生的概率,这样的话就得到: \[f(E(x)) \leqslant E(f(x))\]
寻找下界
我们继续求 \(P(x\ |\ \theta)\) 的下界。
令 \(Q_i\) 是 \(z\) 的某一个分布,\(Qi≥0\),应用Jesen不等式有:
\[\begin{array}{lcl} l(\theta) = \sum_{i=1}^m\log \sum_z p(x,z;\theta) \\ \ \ \ \ \ \ = \sum_{i=1}^m\log \sum_{z^{(i)}} p(x^{(i)},z^{(i)};\theta) \\ \ \ \ \ \ \ = \sum_{i=1}^m\log \sum_{z^{(i)}} Q_i(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \\ \ \ \ \ \ \ \geqslant \sum_{i=1}^m \sum_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \end{array}\]
最后那个式子即为我们要寻找的下界,为了使等号成立,\(\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\) 需要是一个常数,即
\[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} = C\]
进一步分析,为了满足Jessen不等式,还需要 \(\sum_zQ_i(z^{(i)}) = 1\),所以 \(Q_i(z^{(i)})\) 应该能约掉 \(p(x^{(i)},z^{(i)}; \theta)\),并且进行归一化:
\[\begin{array}{lcl} Q_i(z^{(i)}) = \frac{p(x^{(i)},z^{(i)};\theta)}{\sum_zp(x^{(i)},z^{(i)};\theta)} \\ \ \ \ \ \ \ \ \ \ \ \ = \frac{p(x^{(i)},z^{(i)};\theta)}{p(x^{(i)};\theta)} \\ \ \ \ \ \ \ \ \ \ \ \ = p(z^{(i)}\ |\ x^{(i)}; \theta) \end{array}\]
解出来就是一个条件概率!
EM算法整体框架
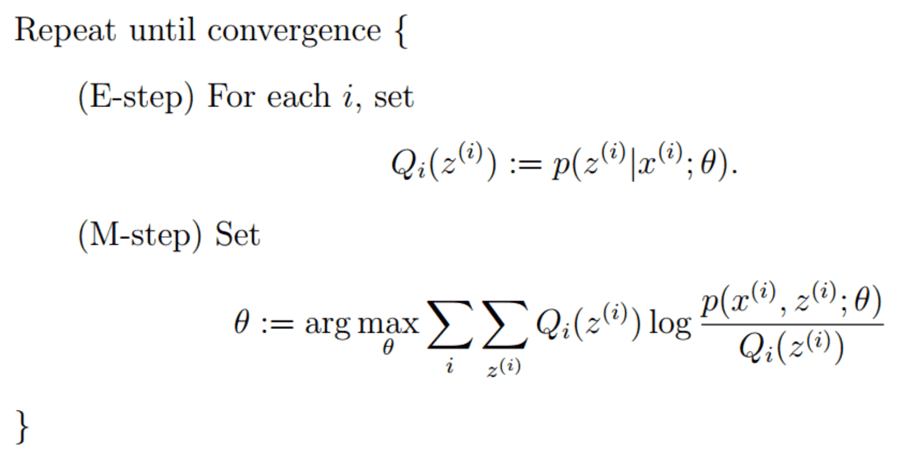
E step,求每组数据的期望(实际是条件概率),然后M setp,最大化期望,之后再翻回去更新期望,如此往复直至收敛,这就是所谓期望最大化算法(EM)。
从理论公式推导GMM
随机变量 \(X\) 是有 \(K\) 个高斯分布混合而成,取各个高斯分布的概率为 \(φ_1φ_2... φ_K\),第 \(i\) 个高斯分布的均值为 \(μ_i\),方差为 \(Σ_i\)。若观测到随机变量 \(X\) 的一系列样本 \(x_1,x_2,...,x_n\),试估计参数 \(φ\),\(μ\),\(Σ\)。
按照EM算法的思想,我们来推导一下。
E-step
\[w_j^{(i)} = Q_i(z^{(i)} = j) = P(z^{(i)} = j\ |\ x^{(i)}; \phi, \mu, \Sigma)\]
M-step
\[\begin{array}{lcl} \ \ \ \sum_{i=1}^m \sum_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\phi, \mu, \Sigma)}{Q_i(z^{(i)})} \\ = \sum_{i=1}^m \sum_{j=1}^k Q_i(z^{(i)} = j)\log\frac{p(x^{(i)}|z^{(i)}=j; \mu, \Sigma)p(z^{(i)}=j; \phi)}{Q_i(z^{(i)} = j)} \\ = \sum_{i=1}^m \sum_{j=1}^k w_j^{(i)}\log \frac{\frac{1}{(2\pi)^{2/n}|\Sigma_j|^{1/2}}\exp(-\frac{1}{2}(x^{(i)}-\mu_j)^T\Sigma_j^{-1}(x^{(i)}-\mu_j))\cdot \phi_j}{w_j^{(i)}} \end{array}\]
其中,\(p(z^{(i)}=j; \phi)\) 为第 \(i\) 个样本的隐变量属于 \(j\) 类的概率,也就是 \(\phi_j\)。
把上式对均值 \(\mu_l\) 求偏导得:
\[\begin{array}{lcl} \ \ \ \bigtriangledown_{\mu_l} \sum_{i=1}^m \sum_{j=1}^k w_j^{(i)}\log \frac{\frac{1}{(2\pi)^{2/n}|\Sigma_j|^{1/2}}\exp(-\frac{1}{2}(x^{(i)}-\mu_j)^T\Sigma_j^{-1}(x^{(i)}-\mu_j))\cdot \phi_j}{w_j^{(i)}} \\ = \bigtriangledown_{\mu_l} \sum_{i=1}^m \sum_{j=1}^k w_j^{(i)} (-\frac{1}{2}(x^{(i)}-\mu_j)^T\Sigma_j^{-1}(x^{(i)}-\mu_j)) \\ = \sum_{i=1}^m w_l^{(i)}(\Sigma_l^{-1}x^{(i)}-\Sigma_l^{-1}\mu_l) \end{array}\]
补充:\(\frac{\partial(x^TAx)}{\partial x} = 2Ax\)
令上式等于 \(0\),解的均值:
\[\mu_l = \frac{\sum_{i=1}^mw^{(i)}_lx^{(i)}}{\sum_{i=1}^mw^{(i)}_l}\]
对 \(\Sigma_j\) 求偏导并令其等于零可以得出:
\[\Sigma_j = \frac{\sum_{i=1}^mw^{(i)}_j(x^{(i)}-\mu_j)(x^{(i)}-\mu_j)^T}{\sum_{i=1}^mw^{(i)}_j}\]
继续对 \(\phi_j\) 求偏导得到:
\[\begin{array}{lcl} \ \ \ \bigtriangledown_{\phi_j} \sum_{i=1}^m \sum_{j=1}^k w_j^{(i)}\log \frac{\frac{1}{(2\pi)^{2/n}|\Sigma_j|^{1/2}}\exp(-\frac{1}{2}(x^{(i)}-\mu_j)^T\Sigma_j^{-1}(x^{(i)}-\mu_j))\cdot \phi_j}{w_j^{(i)}} \\ = \bigtriangledown_{\phi_j} \sum_{i=1}^m \sum_{j=1}^k w_j^{(i)}\log \phi_j \end{array}\]
我们发现令其等于零并不能解出 \(\phi_j\),而且 \(\phi_j\) 还有一个等值约束:\(\sum_{j=1}^k\phi_j = 1\),所以我们用Lagrange乘数法来求解这个约束问题。
建立Lagrange函数
\[L(\phi, \beta) = \sum_{i=1}^m \sum_{j=1}^k w_j^{(i)}\log \phi_j + \beta(\sum_{j=1}^k\phi_j - 1)\]
对Lagrange函数求偏导:
\[\frac{\partial}{\partial \phi_j}L(\phi,\beta) = \sum_{i=1}^m\frac{w^{(i)}_j}{\phi_j} + \beta\]
令其等于零:
\[\begin{array}{lcl} \ \ \ \ \sum_{i=1}^m\frac{w^{(i)}_j}{\phi_j} + \beta = 0 \\ \Rightarrow \sum_{i=1}^m w^{(i)}_j + \beta\cdot \phi_j = 0 \\ \Rightarrow \sum_{j=1}^k\sum_{i=1}^m w^{(i)}_j + \sum_{i=1}^k\beta\cdot \phi_j = 0 \\ \Rightarrow \sum_{i=1}^m\sum_{j=1}^k w^{(i)}_j + \beta = 0 \\ \Rightarrow \sum_{i=1}^m1 + \beta = 0 \\ \Rightarrow \beta = -m \\ \Rightarrow \sum_{i=1}^m\frac{w^{(i)}_j}{\phi_j} -m = 0 \\ \Rightarrow \phi_j = \frac{1}{m}\sum_{i=1}^mw^{(i)}_j \end{array}\]
总结
对于所有的数据点,可以看作组份 \(k\) 生成了这些点。组份 \(k\) 是一个标准的高斯分布,总结上面的结论:
\[\begin{cases} N_k = \sum_{i=1}^N\gamma(i, k) \\ \mu_k = \frac{1}{N_k}\sum_{i=1}^N\gamma(i,k)x_i \\ \Sigma_k = \frac{1}{N_k}\sum_{i=1}^N\gamma(i,k)(x_i - \mu_k)(x_i-\mu_k)^T \\ \pi_k = \frac{N_k}{N} = \frac{1}{N}\sum_{i=1}^N\gamma(i, k) \end{cases}\]
得到了与直观理解GMM一样的公式!