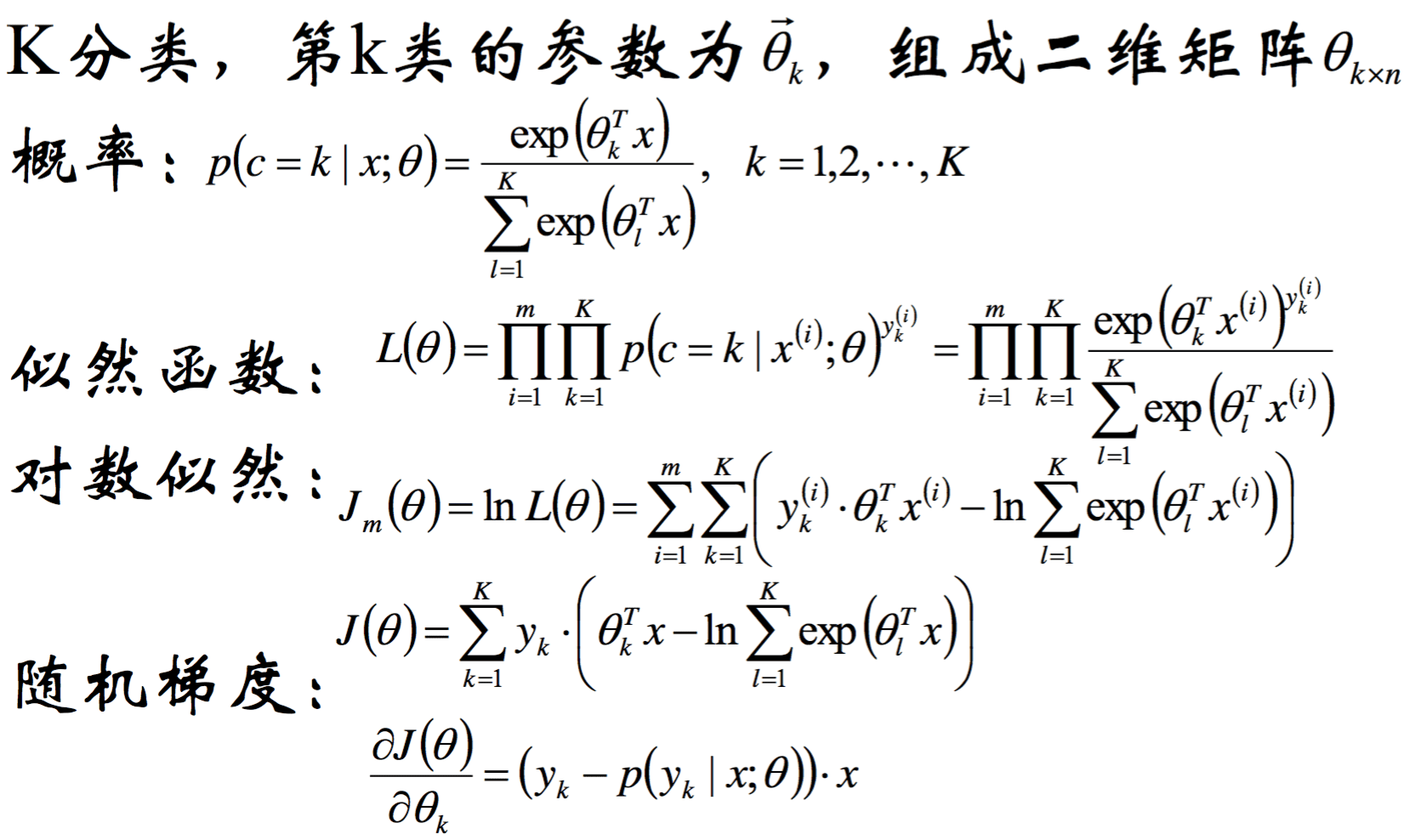使用极大似然估计推导损失函数
回归方程
\[h_\theta(x) = \sum^n_{i=0}\theta_ix_i = \theta^Tx\]
考虑任意一样本 \(y^{(i)}\) ,则有: \[y^{(i)} = \theta^Tx^{(i)} + \epsilon^{(i)}\] 其中 \(\epsilon^{(i)}\) 是误差。
由于每个样本的误差 \(\epsilon^{(i)}\): * 独立同分布(IDD) * 具有有限的数学期望和方差
所以由中心极限定理得:\(\epsilon^{(i)}\) 服从均值为0,方差为某一定值 \(\sigma^2\) 的正态分布。
中心极限定理是概率论中的一组定理。中央极限定理说明,大量相互独立的随机变量,其均值的分布以正态分布为极限。这组定理是数理统计学和误差分析的理论基础,指出了大量随机变量之和近似服从正态分布的条件。 ——from WikiPedia
则 \(\epsilon^{(i)}\) 的概率密度函数为: \[P(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi\sigma}}e^{\frac{-(\epsilon^{(i)})^2}{2\sigma^2}} \]
把 $ ^{(i)} = y^{(i)} - Tx{(i)}$ 代入上式得:
\[ P(y^{(i)}|x^{(i)};\theta) = \frac{1}{\sqrt{2\pi\sigma}}\exp(\frac{-(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2}) \]
\(\because\) 所有样本发生的概率独立同分布 \(\therefore\) 似然函数为所有样本发生概率的乘积,即:
\[\begin{array}{lcl} L(\theta) = \prod^{m}_{i=1} P(y^{(i)}|x^{(i)};\theta) \\ = \prod^{m}_{i=1} \frac{1}{\sqrt{2\pi\sigma}}\exp(\frac{-(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2}) \end{array} \]
在数理统计学中,似然函数是一种关于统计模型中的参数的函数,表示模型参数中的似然性。似然函数在统计推断中有重大作用,如在最大似然估计和费雪信息之中的应用等等。“似然性”与“或然性”或“概率”意思相近,都是指某种事件发生的可能性,但是在统计学中,“似然性”和“或然性”或“概率”又有明确的区分。概率用于在已知一些参数的情况下,预测接下来的观测所得到的结果,而似然性则是用于在已知某些观测所得到的结果时,对有关事物的性质的参数进行估计。 ——from WikiPedia
对 \(L(\theta)\) 取对数得对数似然函数:
\[\begin{array}{lcl} l(\theta) = \log L(\theta) \\ = \log \prod^{m}_{i=1} \frac{1}{\sqrt{2\pi\sigma}}\exp(\frac{-(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2}) \\ = m\log \frac{1}{\sqrt{2\pi\sigma}} + \sum^m_{i=1} \frac{-(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2} \\ = m\log \frac{1}{\sqrt{2\pi\sigma}} - \frac{1}{\sigma^2} \cdot \frac{1}{2} \sum^m_{i=1} (y^{(i)} - \theta^Tx^{(i)})^2 \end{array} \]
若要使对数似然函数取得最大值,把常数项和定值去掉,令 \[J(\theta) = \frac{1}{2}\sum^{m}_{i=1}(y^{(i)} - \theta^Tx^{(i)})^2\] 则 \(J(\theta)\) 应取得最小值, 即为损失函数(目标函数)。
求解最小二乘意义下参数最优解
目标函数
\[ J(\theta) = \frac{1}{2}\sum^{m}_{i=1}(y^{(i)} - \theta^Tx^{(i)})^2 = \frac{1}{2}(X\theta - y)^T(X\theta - y)\]
求梯度
在向量微积分中,标量场的梯度是一个向量场。标量场中某一点的梯度指向在這點标量场增长最快的方向。 —— from WikiPedia
\[\begin{array}{lcr} \nabla_\theta J(\theta) = \frac{\partial}{\partial \theta}(\frac{1}{2}(X\theta - y)^T(X\theta - y)) \\ = \frac{\partial}{\partial \theta}(\frac{1}{2}(\theta^TX^T - y^T)(X\theta - y)) \end{array} \\ = \frac{\partial}{\partial \theta} (\frac{1}{2}(\theta^TX^TX\theta - \theta^TX^Ty - y^TX\theta + y^Ty) ) \\ = \frac{1}{2}(2X^TX\theta - X^Ty - (y^TX)^T) \\ = X^TX\theta - X^Ty \]
标量求梯度 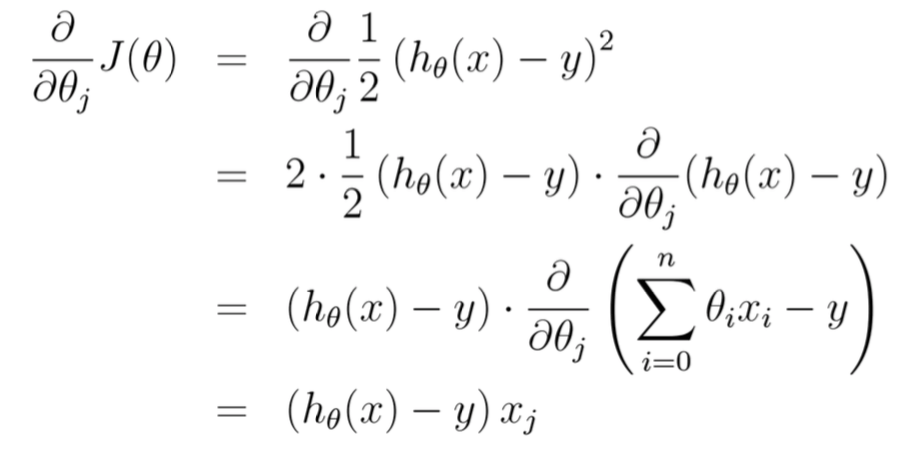
求驻点
令 \(\nabla_\theta J(\theta) = 0\),即 \(X^TX\theta - X^Ty = 0\),解得: \[\theta = (X^TX)^{-1}X^Ty\]
若 \(X^TX\) 不可逆或防止过拟合,增加 \(\lambda\) 扰动: \[\theta = (X^TX + \lambda I)^{-1}X^Ty\]
上两式即为最小二乘意义下的参数最优解。
Logistic 回归的损失函数及参数估计
Sigmoid函数
- $g(z) = $
Sigmoid函数的导数
\[\begin{array}{lcr} g'(z) = (\frac{1}{1 + e^{-z}})' \\ = \frac{e^{-z}}{(1 + e^{-z})^2} \\ = \frac{1}{1 + e^{-z}} - \frac{1}{(1 + e^{-z})^2} \\ = g(z)(1 - g(z)) \end{array} \]
回归方程
- \(h_\theta(x) = g(\theta^TX) = \frac{1}{1 + e^{-\theta^TX}}\)
损失函数
设 $y {1, 0} $ 并且服从二向分布,即:
\[P(y = 1 | x; \theta) = h_\theta(x)\] \[P(y = 0 | x; \theta) = 1- h_\theta(x)\]
则任意样本 \(y^{(i)}\) 的概率密度为
\[P(y^{(i)} | x^{(i)}; \theta) = h_\theta(x^{(i)})^{y^{(i)}}(1 - h_\theta(x^{(i)}))^{1 - y^{(i)}} \]
\(\because\) 所有样本发生的概率独立同分布 \(\therefore\) 似然函数为所有样本发生概率的乘积,即:
\[\begin{array}{lcr} L(\theta) = \prod^{m}_{i=1} P(y^{(i)}|x^{(i)};\theta) \\ = \prod^{m}_{i=1} h_\theta(x^{(i)})^{y^{(i)}}(1 - h_\theta(x^{(i)}))^{1 - y^{(i)}} \end{array} \]
对两边同时取对数得对数似然函数为:
\[\begin{array}{lcr} l(\theta) = \log L(\theta) \\ = \log \prod^{m}_{i=1} h_\theta(x^{(i)})^{y^{(i)}}(1 - h_\theta(x^{(i)}))^{1 - y^{(i)}} \\ = \sum^m_{i = 1} y^{(i)} \log h_\theta(x^{(i)}) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)})) \\ = \sum^m_{i = 1} y^{(i)} \log(\frac{1}{1 + e^{-\theta x^{(i)}}}) + (1 - y^{(i)})\log(\frac{e^{-\theta x^{(i)}}}{1 + e^{-\theta x^{(i)}}}) \\ = \sum^m_{i = 1} y^{(i)} \log(\frac{1}{1 + e^{-\theta x^{(i)}}}) + (1 - y^{(i)})\log(\frac{1}{1 + e^{\theta x^{(i)}}}) \\ \end{array} \]
令 $J() = -l() = ^m_{i = 1} y^{(i)} (1 + e{-x{(i)}}) + (1 - y^{(i)})(1 + e{x{(i)}}) $,即为logistic回归的损失函数。
若令 $y {1, -1} $,进行同样的推导可得另一种形式的损失函数:
\[J(\theta) = \sum^m_{i = 1} \log(1 + e^{-y^{(i)}\theta x^{(i)}}) \]
证明如下:
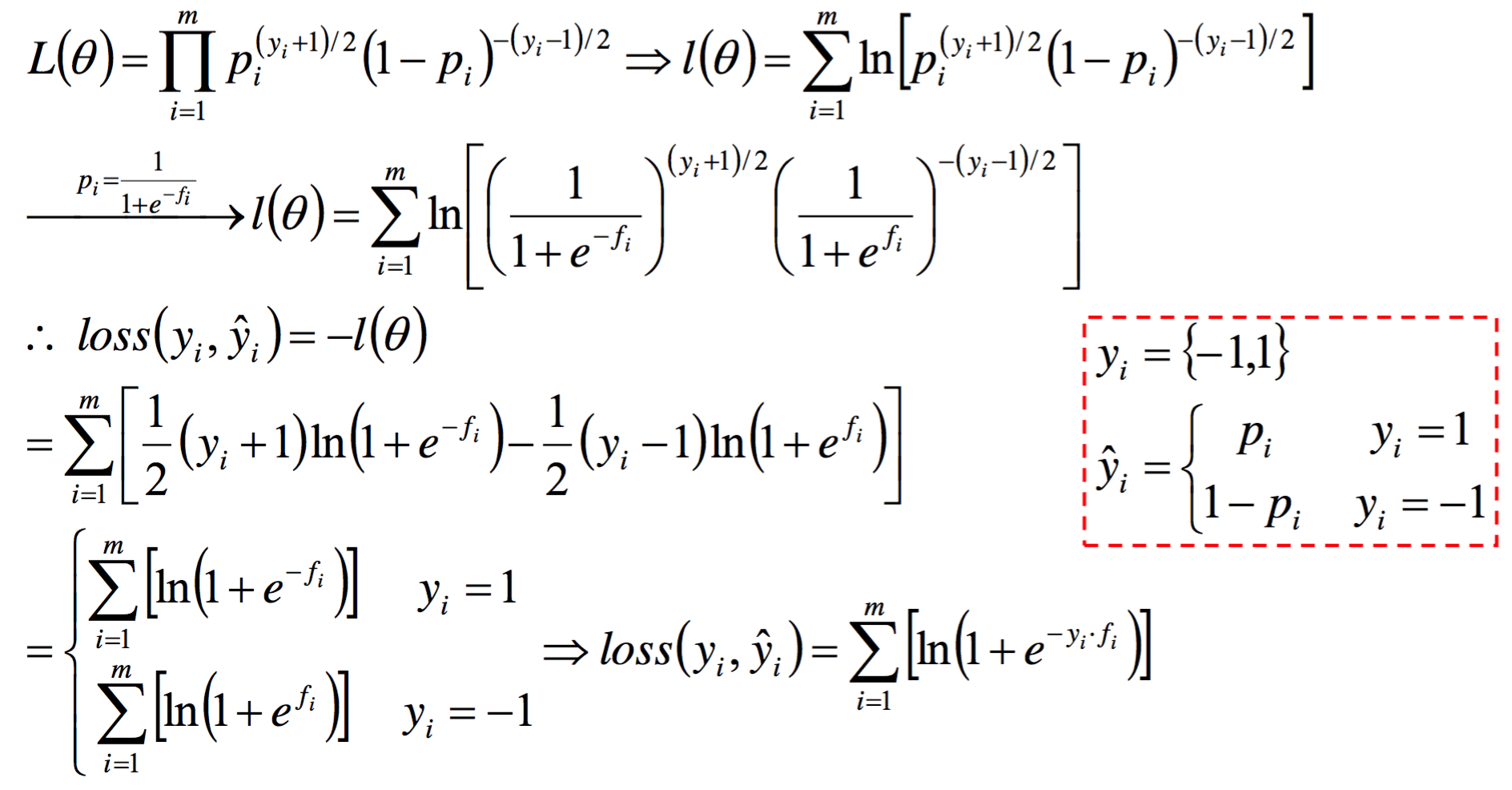
参数估计
求梯度,对对数似然函数(损失函数)对 \(\theta\) 求偏导得 :
\[\begin{array}{lcr} \frac{\partial}{\partial \theta_j}l(\theta) = \frac{\partial}{\partial \theta_j}\sum^m_{i = 1} y^{(i)} \log h_\theta(x^{(i)}) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)})) \\ = \sum^m_{i = 1} y^{(i)}\frac{1}{h_\theta(x^{(i)})}\frac{\partial h_\theta(x^{(i)})}{\partial \theta_j} + (1 - y^{(i)}) \frac{1}{1 - h_\theta(x^{(i)})}\frac{-\partial h_\theta(x^{(i)})}{\partial \theta_j} \\ = \sum^m_{i = 1} y^{(i)}(1 - h_\theta(x^{(i)}))x_j^{(i)} - (1 - y^{(i)}) h_\theta(x^{(i)})x_j^{(i)} \\ = \sum^m_{i = 1} (y^{(i)} - h_\theta(x^{(i)}))x_j^{(i)} \end{array} \]
所以参数的学习规则为:
\[\theta_j := \theta_j + \alpha(y^{(i)} - h_\theta(x^{(i)}))x_j^{(i)} \]
与线性回归的更新规则相同!
对数线性模型

Softmax 回归